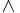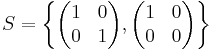Semigroup with two elements
In mathematics, a semigroup with two elements is a semigroup for which the cardinality of the underlying set is two. There are exactly five distinct nonisomorphic semigroups having two elements:
- O2, the null semigroup of order two,
- LO2 and RO2, the left zero semigroup of order two and right zero semigroup of order two, respectively,
- ({0,1}, ∧) (where "∧" is the logical connective "and"), the non-null semigroup with zero of order two,
- (Z2, +2) (where Z2 = {0,1} and "+2" is "addition modulo 2"): the group of order two.
The semigroups LO2 and RO2 are antiisomorphic. O2, ({0,1}, ∧) and (Z2, +2) are commutative, LO2 and RO2 are noncommutative. LO2, RO2 and ({0,1}, ∧) are bands and also inverse semigroups.
Determination of semigroups with two elements
Choosing the set A = { 1, 2 } as the underlying set having two elements, sixteen binary operations can be defined in A. These operations are shown in the table below. In the table, a matrix of the form
indicates a binary operation on A having the following Cayley table.
List of binary operations in { 1, 2 }
|
|
|
|
|
| Null semigroup O2 |
≡ Semigroup ({0,1}, 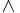 ) ) |
2·(1·2) = 2, (2·1)·2 = 1 |
Left zero semigroup LO2 |
|
|
|
|
|
| 2·(1·2) = 1, (2·1)·2 = 2 |
Right zero semigroup RO2 |
≡ Group (Z2, +2) |
≡ Semigroup ({0,1}, 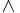 ) ) |
|
|
|
|
|
| 1·(1·2) = 2, (1·1)·2 = 1 |
≡ Group (Z2, +2) |
1·(1·1) = 1, (1·1)·1 = 2 |
1·(2·1) = 1, (1·2)·1 = 2 |
|
|
|
|
|
| 1·(1·1) = 2, (1·1)·1 = 1 |
1·(2·1) = 2, (1·2)·1 = 1 |
1·(1·2) = 2, (1·1)·2 = 1 |
Null semigroup O2 |
In this table:
- The semigroup ({0,1},
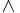 ) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and they make A semigroups all of which are isomorphic to the semigroup ({0,1},
) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and they make A semigroups all of which are isomorphic to the semigroup ({0,1}, 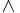 ).
).
- The two binary operations defined by matrices in a blue background are associative and they make A semigroups both of which are isomorphic to the null semigroup O2 with two elements.
- The binary operation defined by the matrix in a yellow background is associative and it makes a A semigroup. This is the left zero semigroup LO2.
- The binary operation defined by the matrix in a pink background is associative and it makes A a semigroup. This is the left zero semigroup LO2 and the other is a right zero semigroup RO2.
- The two binary operations defined by matrices in a brown background are associative and they make A semigroups both of which are isomorphic to the group (Z2, +2).
- The remaining eight binary operations defined by matrices in a white background are not associative and hence they do not make A semigroups.
The two-element semigroup ({0,1}, 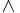 )
)
The Cayley table for the semigroup ({0,1}, 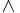 ) is given below:
) is given below:
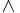 |
0 |
1 |
| 0 |
0 |
0 |
| 1 |
0 |
1 |
This is the simplest non-trivial example of a semigroup that is not a group. This semigroup is commutative and has an identity element, which is 1 . It is not a group because the element 0 does not have an inverse. In fact, it is not even a cancellative semigroup because we cannot cancel the 0 in the equation 1·0 = 0·0.
This semigroup arises in various contexts. For instance, if we choose 1 to be the truth value "true" and 0 to be the truth value "false" and the operation to be the logical connective "and", we obtain this semigroup in logic. It is also isomorphic to the semigroup
under matrix multiplication.[1]
The two-element semigroup (Z2,+2)
The Cayley table for the semigroup (Z2,+2) is given below:
This group is isomorphic to the symmetric group S2.
Finite semigroups of higher orders
Let A be the three-element set { 1, 2, 3 }. Altogether, a total of 39 = 19683 different binary operations can be defined on A. It is impractical to prepare a list of all these binary operations, and determine those that make A nonisomorphic semigroups. Algorithms and computer programs have been developed for determining nonisomorphic finite semigroups of a given order. These have been applied to determine the nonisomorphic semigroups of order three or higher.[2][3] In fact, 113 of the 19683 binary operations determine 24 nonisomorphic semigroups, or 18 non-equivalent semigroups (with equivalence being isomorphism or anti-isomorphism). The number of nonisomorphic semigroups with n elements, for n a nonnegative integer, is listed under A027851 in the On-Line Encyclopedia of Integer Sequences. A001423 lists the number of non-equivalent semigroups, and A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.
See also
References
- ^ This article incorporates material from Semigroup with two elements on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
- ^ Siniša Crvenkovič; Ivan Stojmenovic. An algorithm for Cayley tables of algebras. 23. Univ. u Novom Sadu, Zb. Rad. Prirod.-Mat. Fak. Review of Research, Faculty of Science. pp. 221–231. [1] (Accessed on 09 May 2009)
- ^ John A Hildebrant (2001). Handbook of Finite Semigroup Programs. (Preprint). [2]
 )
)  )
)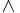 ) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and they make A semigroups all of which are isomorphic to the semigroup ({0,1},
) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and they make A semigroups all of which are isomorphic to the semigroup ({0,1}, 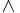 ).
).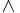 )
)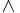 ) is given below:
) is given below: